11660번: 구간 합 구하기 5 - Kotlin

https://www.acmicpc.net/problem/11660

11660번: 구간 합 구하기 5

문제

N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.

예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

 

1	2	3	4
2	3	4	5
3	4	5	6
4	5	6	7

 

여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.

표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.

입력

첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)

출력

총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.

 

나의 풀이 - 1차 (시간 초과)

 이 문제는 구간합과 DP를 이용해야 하는 문제이다. 나는 행으로 구간합을 저장하고 그 값을 구하려고 하였다. 그 방법은 다음과 같다. 예시로 주어진 2,2 부터 4, 3까지의 구간합을 구해보겠다. 아래의 표와 같다

 

 

 

 

 

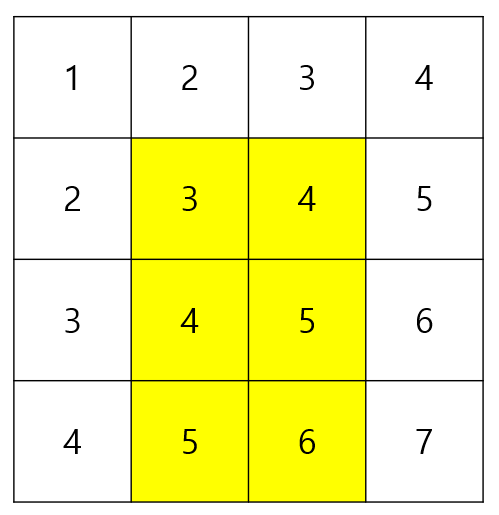
 나는 가로로 구간합을 구하려고 하였기에 위의 줄에서 구간합을 구하려면

 3번째 줄까지의 합 - 1번째 줄까지의 합을 해야 내가 원하는 2,2부터 2,3의 구간합을 구할 수 있다. 이 과정을 모든 줄에서 반복하였다/

 

하지만 이 방식은 시간 초과가 발생하고 말했다. 해서 다른 방식을 찾거나 시간을 줄일 수 있는 방법을 찾아야 한다.

 

fun main() = with(System.`in`.bufferedReader()) {
    val (n, m) = readLine().split(" ").map { it.toInt() }

    val graph = Array(n) { readLine().split(" ").map { it.toInt() }.toIntArray() }
    val problem = Array(m) { readLine().split(" ").map { it.toInt() - 1 }.toIntArray() }

    val dp = Array(n) { IntArray(n) }

    for (i in 0 until n) {
        dp[i][0] = graph[i][0]
        for (j in 1 until n) {
            dp[i][j] = graph[i][j] + dp[i][j - 1]
        }
    }

    problem.forEach {
        var sum = 0
        for (i in it[0]..it[2]) {
            if (it[1] == 0)
                sum += dp[i][it[3]]
            else
                sum += (dp[i][it[3]] - dp[i][it[1] - 1])
        }
        println(sum)
    }
}

 

 

나의 풀이 - 2차

 이전에는 행으로 구간합을 구하려고 하였다. 그런데 그냥 2차원 배열에서 구간합을 구하는 방법이 있었다. 이전의 방식과 거의 유사한데 나중에 조건을 좀 더 줘야하는 점이 다른점이다.

 

fun main() = with(System.`in`.bufferedReader()) {
    val (n, m) = readLine().split(" ").map { it.toInt() }

    val graph = Array(n) { readLine().split(" ").map { it.toInt() }.toIntArray() }
    val problem = Array(m) { readLine().split(" ").map { it.toInt() - 1 }.toIntArray() }

    for (i in 0 until n) {
        for (j in 1 until n) {
            graph[i][j] += graph[i][j - 1]
        }
    }

    for (j in 0 until n) {
        for (i in 1 until n) {
            graph[i][j] += graph[i - 1][j]
        }
    }

    for (i in problem) {
        if (i[0] == 0 && i[1] == 0) {
            println(graph[i[2]][i[3]])
            continue
        }
        if (i[0] == 0) {
            println(graph[i[2]][i[3]] - graph[i[2]][i[1] - 1])
            continue
        }
        if (i[1] == 0) {
            println(graph[i[2]][i[3]] - graph[i[0] - 1][i[3]])
            continue
        }
        println(graph[i[2]][i[3]] - graph[i[0] - 1][i[3]] - graph[i[2]][i[1] - 1] + graph[i[0] - 1][i[1] - 1])
    }
}