프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.

또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.
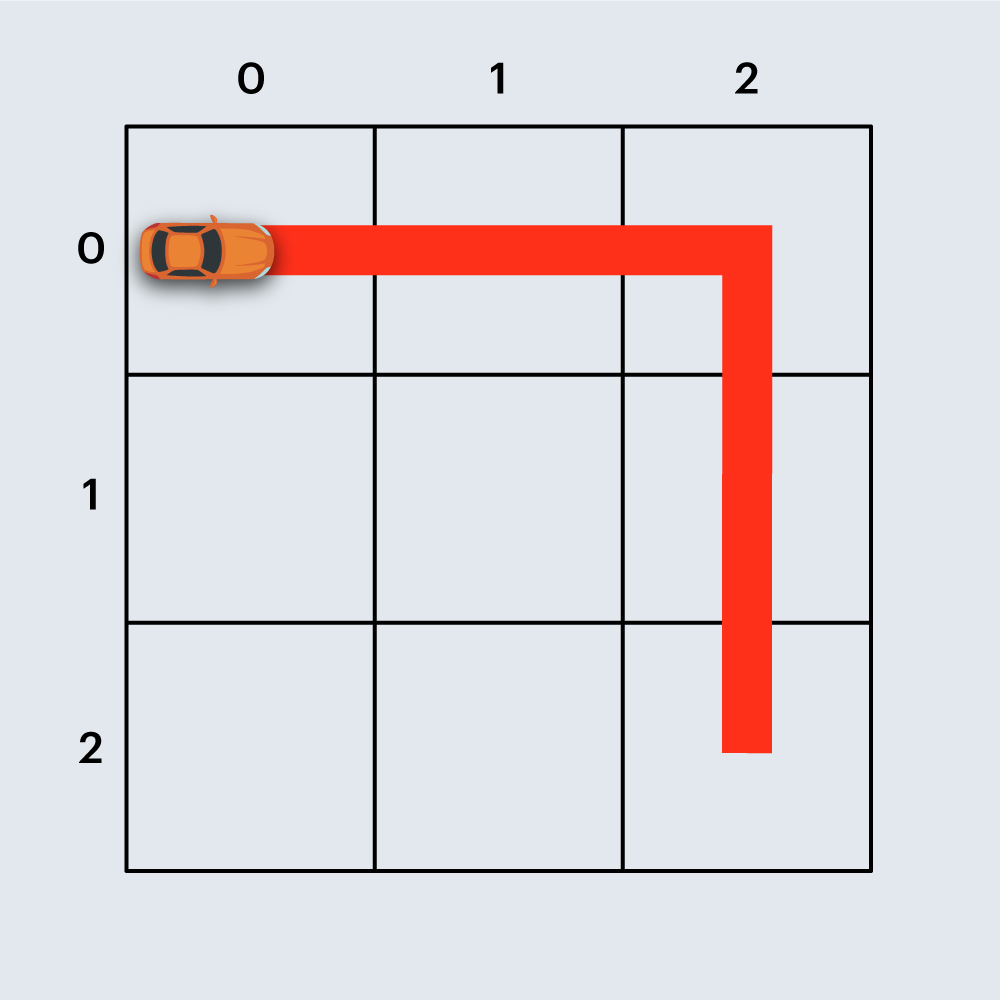
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
나의 풀이
이 문제는 BFS를 이용해야 하는 문제이다. 다만 각 방향에 따라 경우의 수가 다르기 때문에 해당하는 위치에 어떤 방향으로 들어왔는지를 다 고려해야만 한다. 이 부분만 고려할 수 있다면 문제를 해결할 수 있다.
(각 방향에 따른 경우의 수를 고려하지 않는다면 25번 테스트 케이스가 실패한다)
import java.util.*
import kotlin.math.*
class Solution {
val dx = arrayOf(0, 1, 0 ,-1)
val dy = arrayOf(1, 0, -1, 0)
fun solution(board: Array<IntArray>): Int =
bfs(board.size, board)
data class Car(val x: Int, val y: Int, val cost: Int, val direct: Int)
fun bfs(n: Int, board: Array<IntArray>): Int {
val queue : Queue<Car> = LinkedList()
val visited = Array(n) { Array(n) { IntArray(4) { Int.MAX_VALUE / 2 } } }
queue.add(Car(0, 0, 0, -1))
while (queue.isNotEmpty()) {
val (x, y, cost, direction) = queue.poll()
for (i in 0..3) {
val tempX = x + dx[i]
val tempY = y + dy[i]
val next = if (direction == i || direction == -1)
cost + 100
else
cost + 600
if (tempX in 0 until n &&
tempY in 0 until n &&
board[tempX][tempY] != 1) {
if (visited[tempX][tempY][i] >= next) {
visited[tempX][tempY][i] = next
queue.add(Car(tempX, tempY, next, i))
}
}
}
}
var answer = Int.MAX_VALUE / 2
visited[n - 1][n - 1].forEach {
answer = min(answer, it)
}
return answer
}
}'프로그래머스 - kotlin > LEVEL 3' 카테고리의 다른 글
| 가장 긴 팰린드롬 - Kotlin (0) | 2023.06.25 |
|---|---|
| 입국 심사 - Kotlin (이분 탐색) (0) | 2023.06.25 |
| 디스크 컨트롤러 - Kotlin (우선순위 큐) (0) | 2023.06.20 |
| 여행 경로 - Kotlin (DFS) (0) | 2023.06.19 |
| 섬 연결하기 - Kotlin (최소 스패닝 트리) (0) | 2023.06.19 |
