배낭 문제란?
배낭 문제는 조합 최적화 문제의 일종이다. 간략하게 말하자면, 담을 수 있는 최대 무게가 정해진 배낭과 함께 각각의 무게와 가치가 주어진 아이템의 집합이 주어졌을 때, 배낭에 담은 아이템들의 가치의 합이 최대가 되도록 하는 아이템들의 부분집합을 찾는 문제이다.
우리가 흔히 쓰는 배낭 문제는
- Fraction Knapsack Problem
- 0-1 Knapsack Problem
이 2가지가 존재한다.
Fraction Knapsack Problem (분할 가능한 배낭 문제) with Greedy Algorithm
내가 배낭 문제를 처음 접했을때 든 생각은 "어 이거 그리디 알고리즘 아닌가?" 였다.
그리디 알고리즘에서 가장 유명한 문제인 동전 거스름돈 문제는 일단 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한이 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러 줘야 할 동전의 최소의 개수를 구하는 문제이다. 매우 간단하게 해결할 수 있는 문제이지만, 이 문제에는 엄청난 맹점이 존재한다.
만약 손님에게 800원을 거슬러줘야 한다면, 그리디 알고리즘은 가장 큰 수부터 거슬러주기 시작해 500원 하나와 100원짜리 동전을 3개 거슬러 줄 것이다. 하지만 만약에 400원짜리 동전이 존재한다고 가정해보자. 400원짜리 동전으로 800원을 거슬러준다면 동전이 2개가 필요함으로 이 방식이 가장 적은 동선의 개수를 이용한 방식이 된다.
다시 분할 가능한 배낭 문제로 돌아와보자.

그림과 같은 열린 상자에 든 금괴를 도둑이 훔처간다고 가정해보자. 이 때 도둑은 자신의 배낭에 15kg를 담을 수 있고, 가치가 다른 5가지의 상자가 존재한다. 이때 도둑이 배낭에 담을 수 있는 최적의 조합은 C 4kg, B 1kg, E 2kg, D 1kg, A 7kg가 된다. 이런 형태의 문제를 분할 가능한 배낭 문제라고 한다.
이 문제는 위에서 설명했었던 그리디 알고리즘으로 해결가능하다. 그래서 내가 처음 배낭 문제를 접했을때 처음처럼 생각했던 이유였다. 동전문제와 위의 예시 문제의 차이라면, 동전 문제는 동선의 개수가 무제한이라는 것이다.
0-1 Knapsack Problem
그렇다면 이제는 0-1 배낭 문제에 대하여 알아보겠다.
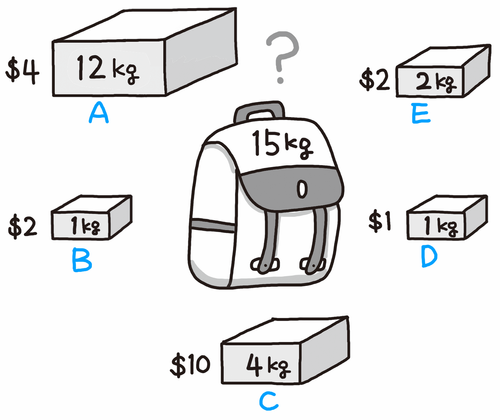
이번에는 열리지 않는 상자에 든 금괴를 훔쳐 간다고 생각해보겠다. 도둑은 전과 같이 15kg를 자신의 배낭에 넣을 수 있을 때, 도둑이 배낭에 담을 수 있는 최적의 조합은 C 4kg, B 1kg, E 2kg, D 1kg 이다. 이전의 담았던 A 상자의 금괴는 담을 수 없다. 0-1 배낭 문제는 그 물건을 포함하거나 아니면 포함하지 않거나 둘 중 하나의 선택만을 할 수 있기 때문에 A 상자를 열어서 일부를 꺼낼 수 없다. 이런 형태의 문제를 0-1 배낭 문제라고 한다.
이런 0-1 배낭 문제는 DP 나 Backtracking 등의 조합 최적화 문제의 풀이 방법으로 해결할 수 있다.
그럼 이제 배낭 문제를 직접 풀어보면서 깊은 이해를 하는 과정을 가지겠다.
12865번: 평범한 배낭
12865번: 평범한 배낭 - Kotlin
12865번: 평범한 배낭 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의
everyday-develop-myself.tistory.com
Reference
https://namu.wiki/w/%EB%B0%B0%EB%82%AD%20%EB%AC%B8%EC%A0%9C
'개발자의 기본 소양 > ALGORITHM' 카테고리의 다른 글
| Topological sort (위상 정렬) with 2252번: 줄 세우기 - Kotlin (0) | 2023.03.25 |
|---|---|
| Euclidean algorithm (유클리드 호제법) (0) | 2023.03.03 |
| BackTracking with 9663번: N-Queen (0) | 2023.02.24 |
| Floyd-Warshall Algirithm (플로이드 워셜 알고리즘) (0) | 2023.02.23 |
| Dijkstra Algorithm (다익스트라 알고리즘) with 프로그래머스 - 배달 (0) | 2023.02.23 |
