12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
문제
이 문제는 아주 평범한 배낭에 관한 문제이다.
한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
입력
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.
출력
한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.
나의 풀이
이 문제는 분할이 불가능한 물품을 배낭에 넣어야 하는 문제임으로 배낭 문제중 0-1 Knapsack Problem인것을 알 수 있다. 이 문제는 DP를 통하여 해결이 가능하다.
이 문제는 2가지의 배열과 하나의 2차원 배열이 필요하다. 무게를 담은 w 배열, 가치를 담은 v 배열을 두었고 반복문을 수행하면서 값을 넣어줄 dp 2차원 배열을 선언하였다.
이 문제의 핵심은 j라는 배낭이 감당할 수 있는 최대 무게 안에서 i번째의 물건을 직접 넣어보는 것이다. i, j는 1부터 N까지 dp 2차원 배열의 모든 장소에 값을 할당해 줌으로 다시 앞으로 돌아와서 계산을 할 필요가 없이 나중에 필요한 값을 불러오기만 하면 된다. 만약 최대 무게 안에 물건이 2개 이상 들어간다고 한다면 바로 전에 최대 무게의 배낭안에 들어갔던 물건의 가치와 지금 i에 해당하는 무게를 가방에 넣고 남은 무게만큼 물건을 넣었던 이전의 기록을 가져와서 비교를 하게 된다.
그림으로 예를 한번 들어보겠다. 현재 가방의 최대 무게 j가 7일때 물건을 넣는 경우를 생각해보자.
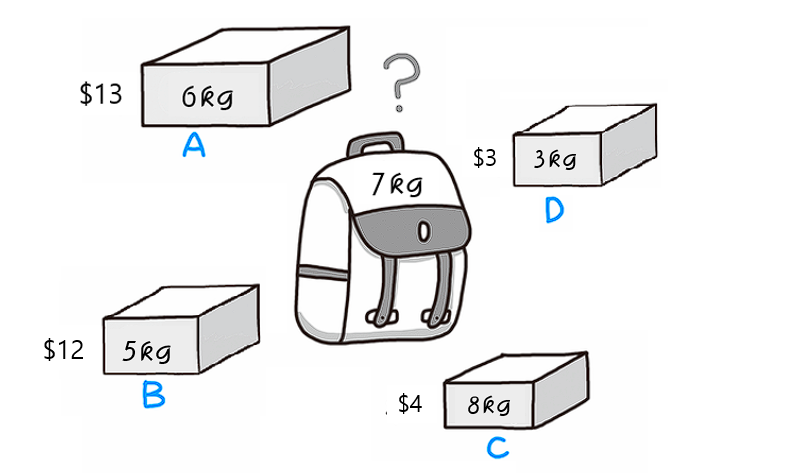
1. i = 0
i가 0일때는 주어진 범위가 아님으로 d[0][7] = 0 이 된다.
2. i = 1
i가 1일때는 w[1] = 6kg, v[1] = 13 이다. 이때 가방의 최대 무게 7kg보다 w[1]이 작다. 이때는 바로 위에서 구했던 d[0][7]의 값과 가방에 6kg을 넣었을때 남은 값인 1kg가 최대 무게였을 때의 값인 d[0][1]의 가치를 더한 결과를 비교하여 더 큰 값을 d[1][7]에 넣게 된다. 이때는 d[0][7] = 0이고 d[0][1] + v[1] = 0 + 13 = 13임으로 d[1][7] = 13이 되게 된다.
3. i = 2
i가 2일때 값은 1일때 값을 구했을때랑 유사하다. 계산을 하게되면 d[2][7] = 13이 된다.
3. i = 3
i가 3일때는 w[3] = 3kg, v[3] = 6 이다. 이때 가방의 최대 무게보다 w[3]이 작고 이때 위에서 구했던 방식대로 수식을 써보면 d[2][7]의 값과 3kg만큼 가방에 물건을 넣었을때 남은 무게인 4kg가 최대 무게였을 때의 값인 d[2][4]와 v[3]의 합을 비하게 된다. d[2][7] = 13이고 d[2][4] + v[3] = 8 + 6 = 14임으로 d[3][7] = 14가 된다.
이런 방식으로 0-1 Knapsack Problem이 진행되게 된다. 이제 남은 것은 위의 내용을 코드로 작성하는 것이다.
import kotlin.math.max
fun main() = with(System.`in`.bufferedReader()) {
val (n, k) = readLine().split(" ").map { it.toInt() }
val w = IntArray(n + 1)
val v = IntArray(n + 1)
for (i in 1 until n + 1) {
val (W, V) = readLine().split(" ").map { it.toInt() }
w[i] = W
v[i] = V
}
val dp = Array(n + 1) { IntArray(k + 1) }
for (i in 1..n) {
for (j in 1..k) {
if (w[i] > j)
dp[i][j] = dp[i - 1][j]
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
}
}
println(dp[n][k])
}
'백준 > DP' 카테고리의 다른 글
| 1520번: 내리막 길 - Kotlin (0) | 2023.03.24 |
|---|---|
| 11053번: 가장 긴 증가하는 부분 수열 (0) | 2023.03.02 |
| 9095번: 1, 2, 3 더하기 - Kotlin (0) | 2023.03.02 |
| 1463번: 1로 만들기 - Kotlin (0) | 2023.03.02 |
| 9251번: LCS - Kotlin (0) | 2023.02.27 |
