2096번: 내려가기
첫째 줄에 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 숫자가 세 개씩 주어진다. 숫자는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 중의 하나가 된다.
www.acmicpc.net
문제
N줄에 0 이상 9 이하의 숫자가 세 개씩 적혀 있다. 내려가기 게임을 하고 있는데, 이 게임은 첫 줄에서 시작해서 마지막 줄에서 끝나게 되는 놀이이다.
먼저 처음에 적혀 있는 세 개의 숫자 중에서 하나를 골라서 시작하게 된다. 그리고 다음 줄로 내려가는데, 다음 줄로 내려갈 때에는 다음과 같은 제약 조건이 있다. 바로 아래의 수로 넘어가거나, 아니면 바로 아래의 수와 붙어 있는 수로만 이동할 수 있다는 것이다. 이 제약 조건을 그림으로 나타내어 보면 다음과 같다.

별표는 현재 위치이고, 그 아랫 줄의 파란 동그라미는 원룡이가 다음 줄로 내려갈 수 있는 위치이며, 빨간 가위표는 원룡이가 내려갈 수 없는 위치가 된다. 숫자표가 주어져 있을 때, 얻을 수 있는 최대 점수, 최소 점수를 구하는 프로그램을 작성하시오. 점수는 원룡이가 위치한 곳의 수의 합이다.
입력
첫째 줄에 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 숫자가 세 개씩 주어진다. 숫자는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 중의 하나가 된다.
출력
첫째 줄에 얻을 수 있는 최대 점수와 최소 점수를 띄어서 출력한다.
나의 풀이
이 문제는 DP를 사용해야 하는 문제이다. 문제의 풀이는 생각보다 간단하다.
DP를 풀 때 가장 먼저 생각해야 하는 것은 내가 원하는 값을 그 이전의 값으로 어떻게 나타낼 수 있는지 고려하는 것이다.
3의 행을 가진 2차원 배열을 나타내 보겠다
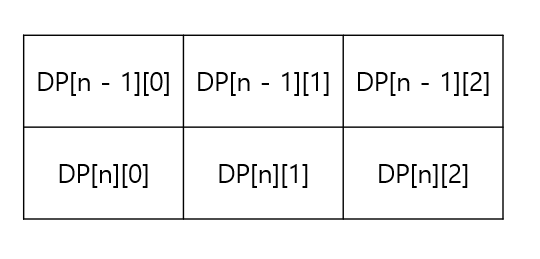
우리가 구하고 싶은 값은 마지막 줄인 DP[n][0], DP[n][1], DP[n][2]의 최대값이다.
1) DP[n][0] 일 때
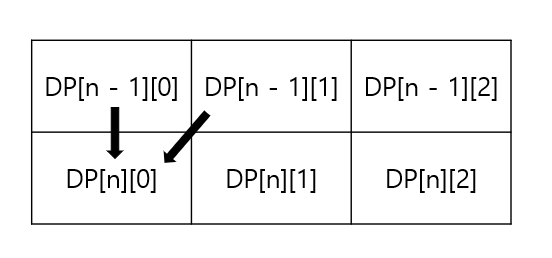
DP[n][0]으로 갈 수 있는 방법은 DP[n - 1][0]과 DP[n - 1][1] 밖에 없다. 이 둘의 합이 바로 DP[n][0]의 최대값이 된다는 말이다.
2) DP[n][1] 일 때
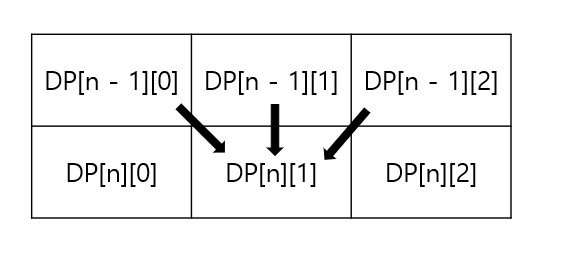
DP[n][1]으로 갈 수 있는 방법은 DP[n - 1][0]과 DP[n - 1][1], DP[n - 1][2]가 있다. 이 셋의 합이 바로 DP[n][01의 최대값이 된다는 말이다.
이제 어떻게 하는지 이해했을 것이라 믿는다. 최대와 최소는 max와 min 사용하면 된다. 코드는 다음과 같다.
import kotlin.math.max
import kotlin.math.min
fun main() = with(System.`in`.bufferedReader()) {
val n = readLine().toInt()
val num = Array(n) { readLine().split(" ").map { it.toInt() }.toIntArray() }
var dp = Array(n) { IntArray(3) }
dp[0] = num[0]
for (i in 1 until n) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]) + num[i][0]
dp[i][1] = maxOf(dp[i - 1][0], dp[i - 1][1], dp[i - 1][2]) + num[i][1]
dp[i][2] = max(dp[i - 1][1], dp[i - 1][2]) + num[i][2]
}
print(maxOf(dp[n - 1][0], dp[n - 1][1], dp[n - 1][2]).toString() + " ")
dp = Array(n) { IntArray(3) }
dp[0] = num[0]
for (i in 1 until n) {
dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + num[i][0]
dp[i][1] = minOf(dp[i - 1][0], dp[i - 1][1], dp[i - 1][2]) + num[i][1]
dp[i][2] = min(dp[i - 1][1], dp[i - 1][2]) + num[i][2]
}
println(minOf(dp[n - 1][0], dp[n - 1][1], dp[n - 1][2]))
}
'백준 > DP' 카테고리의 다른 글
| 9184번: 신나는 함수 실행 - Kotlin, Java (0) | 2023.10.01 |
|---|---|
| 2011번: 암호코드 - Kotlin (0) | 2023.06.14 |
| 2565번: 전깃줄 - Kotlin (0) | 2023.06.11 |
| 2225번: 합분해 - Kotlin (0) | 2023.06.07 |
| 11054번: 가장 긴 바이토닉 부분 수열 - Kotlin (1) | 2023.06.06 |
